

Block or stream? That is the question.
Fixed-size blocks. Longer messages are divided to blocks and encrypted accordingly.
Hard to define: usually attacks go around the definition, or it is too strict so no reasonable cipher fits into it.
Idea: the cipher is not distinguishable from a random permutation.
Most ciphers produce only even permutations.
Usually, a cipher is considered secure if
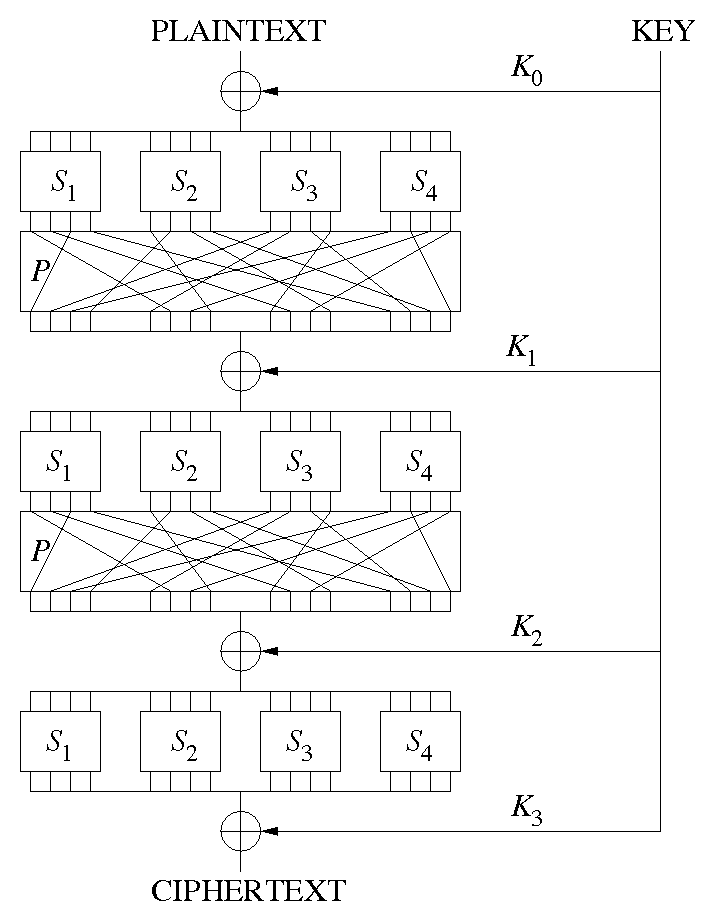
SPNs
S-boxes small lookup tables, invertible
whitening xor at the beginning and at the end. Prevents the attacker from influencing S-boxes.
p-box permutation of the block
upgradable by using some invertible linear transformations instead of permutations
Feistel networks
Construction with noninvertible S-boxes.
Decryption is again a Feistel network, but with reversed key order. This allows some very elegant implementations.
The left and the right part are switched after each round.
History
In the 70s by IBM, ordered by National Bureau for Standards.
56-bit key (or 64 bit but each byte has a parity bit — NSA trolling)
64-bit blocks.
NSA influenced S-boxes to make the cipher stronger.
Structure
Feistel network with 16 rounds working with 32-bit half-blocks.
Initial and Final Permutation (IP & FP) — useless
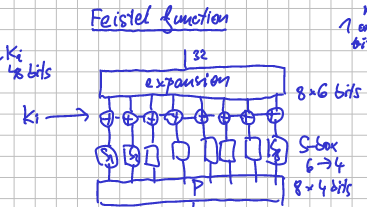
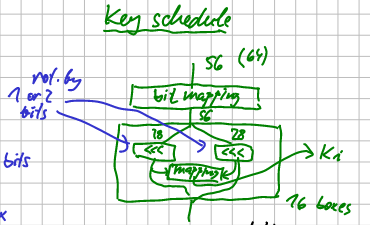
Key schedule
bit mapping
16 boxes
another mapping and we have a round-key
then continue to another box/round
Critique of DES
Kyes: all ones, all zeros,
There also exist key pairs (semi-weak keys)
such that (
DES has complementarity property
Keys are so short that it's unsafe.
you can even pay for a service that breaks DES for you.
Small blocks, collisions every
Differential cryptoanalysis needs
Linear cryptoanalysis
Put all together it’s broken.
Tries to save the day
2-DES won’t help because we can meet-in-the-middle

3-DES
sometimes with
1997 NIST (successor of NBS) announces a competition. They get 15 proposals, it takes a few years to choose the best one.
criteria: security, speed, easiness of implementation
2001 Rijndael wins, renamed AES
128-bit blocks, key 128 (10 rounds), 192 (12) or 256 (14) bits
SPN with linear transformation
inner state and round key are both 4x4 matrices
Round
Before the first round we add round key.
Inverse roundThe following operations commute:
Critique
Very conservative.
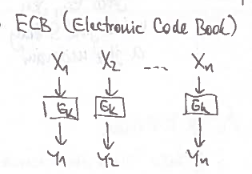
Blocks


Each block is encrypted independently of the other blocks.
If two blocks are identical then the corresponding cipher blocks are the same.
No IV, so it’s deterministic
It is possible to swap blocks, change one block without influencing other
So this is the worst block cipher mode which could be made. — Martin Mareš.
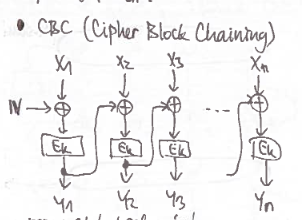
Uses IV.
XORs preceding block to the current.
Decryption can be parallelized and random access. But changes of blocks are not possible because you have to recalculate everything after the changed block.
The most frequently used mode.
Leak
After about
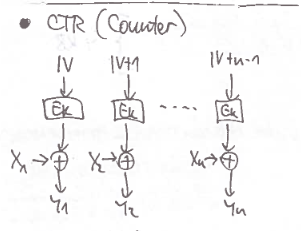
Turns block cipher into a stream cipher.
IVs need to be random (when using the same key).
Easily parallelized.
Leak
Every keystream is different which leaks some fraction of information over a long period of time.
Uses IV and then the output of the preceding key stream is used to create key-stream for the next block.
Problem: we're following some cycle in a permutation, there’s a possibility we hit some short cycle.


The attacker is able to know if the message had a valid padding.
Assume the padding: repeat the byte containing the size of the padding
We will try all the possible values in the last byte of the padding. There is exactly one solution to obtain padding of size 1 in the block. With this, we can recover the size of the original padding. Now we need to recover the previous byte. We’ll be flipping the previous byte until we create in it p+1. Thus, we recovered it. We recover the whole block like this. Then we discard the block and repeat the process on the previous block.
This allows us to recover the block in
Some versions of TLS permit padding oracles.
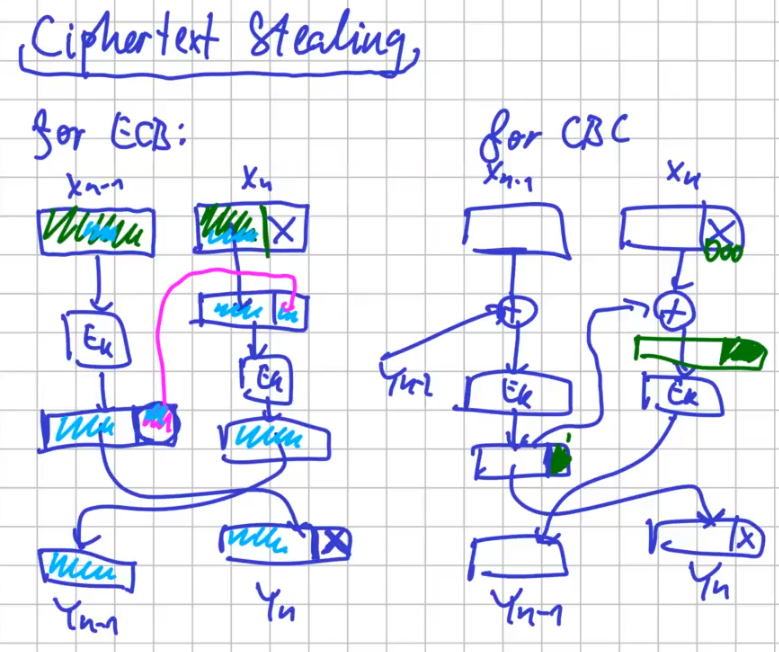
There aren’t many of them.
eSTREAM project
European project that tried to find good SW and HW stream ciphers.
for well-chosen keys, the period is
problem
Known plaintext allows for recovery of the initial state of the register from the first few bits. We can solve it with nonlinear registers!
the next state is determined by a non-linear function of the current.
Usually, it is hard to ensure a long period.
Some workarounds:
Most ciphers based on it are weak. A5/1 — used in GSM and broken.
Uses AND and XOR for nonlinear function.
init:
no known attack with complexity lower than
Interestingly, the computation can be parallelized.

good SW implementation, based on permutating
Believed to be a strong cipher many years ago, but it’s broken through KPA
.A very similar cipher was a finalist of eSTREAM (it was called Salsa20).
Why 20? Well, 20 is the number of rounds.
ChaCha20 produces 1 block of keystream (and it isn’t bijective) given the following params:
It is similar to CTR mode.
Internal state is a 4x4 matrix of 32-bit values
ARX stands for addition, rotation, XOR. After 20 rounds of this, magic it should produce a good pseudorandom keystream. The output of this is summed with the initial state so it's uninvertible.